Efficient Coding

Principles and Practices for Performant Code

Eirini & Rhian, DS @ SU

Agenda

• Measuring Performance: Time and profile your code
• Common Performance Tweaks: Easy wins for faster code
• Loops vs. Vectorisation vs. …: Choose the right approach
• Optimising Loops: When you should use them
• Beyond the Basics: Tools for further optimisation

Measuring Performance

Timing

• How long does it take?
• Can compare approaches?
• When will your code finish running when you scale it up?

🐍 Timing

from timeit import timeit

size = 100_000

def sum_of_squares():
    return sum(i**2 for i in range(size))

execution_time = timeit('sum_of_squares()',
                       globals=globals(),
                       number=100)

print(f"Average execution time: {execution_time/1000:.6f}s")

🦜 Timing

• system.time() for quick one-off timing
• {bench} for parameterised comparisons

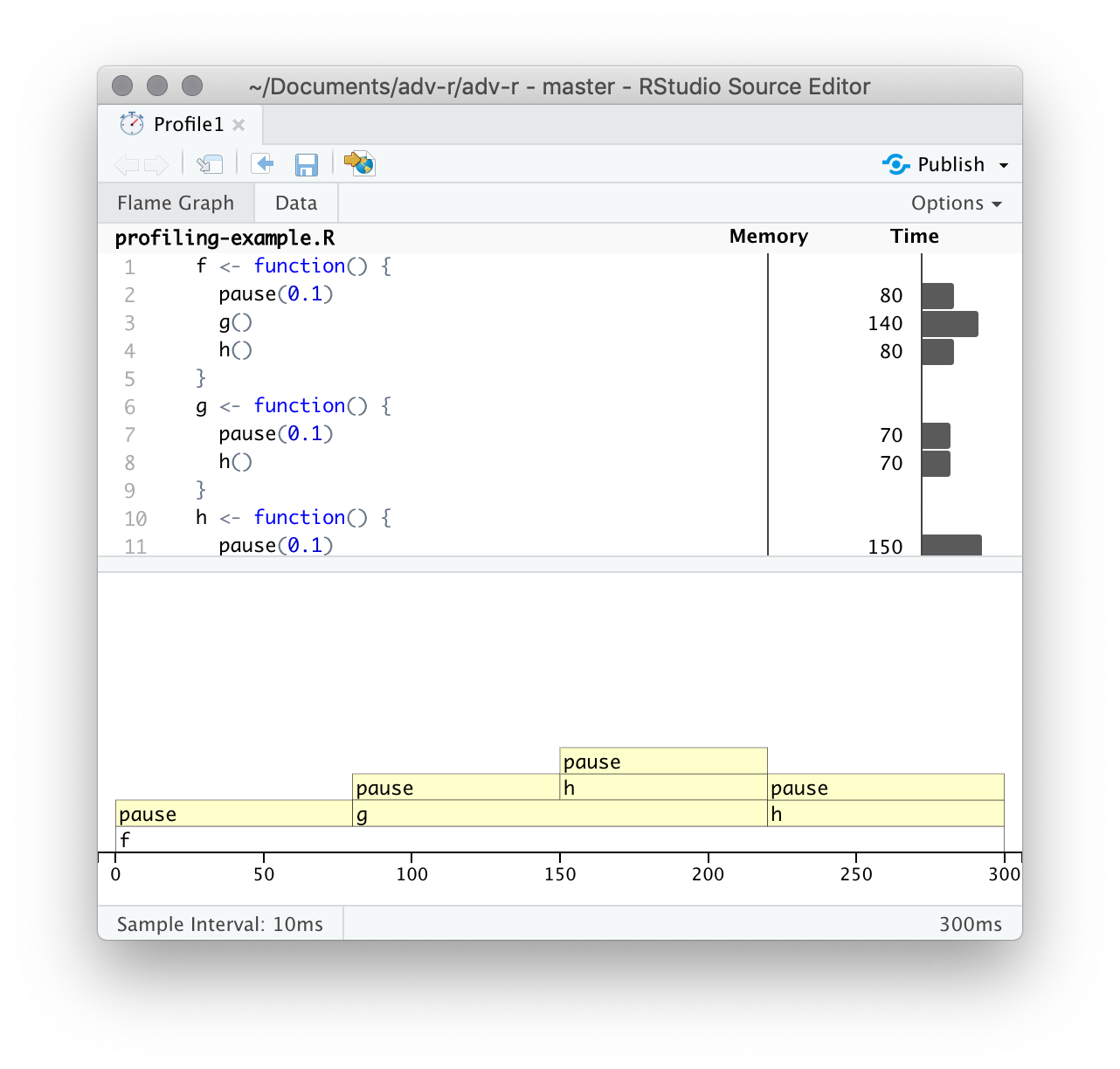
Profiling

“We should forget about small efficiencies, say about 97% of the time: premature optimization is the root of all evil.” - Donald Knuth

• Identify the slowest functions

🐍 Profiling

from random import uniform
from pyinstrument import Profiler

# Monte Carlo method estimating pi through simulation and geometric probability
def hits(point):
    return abs(point) <= 1

def point():
    return complex(uniform(0, 1), uniform(0, 1))

def estimate_pi(n):
    return 4 * sum(hits(point()) for _ in range(n)) / n

with Profiler(interval=0.1) as profiler:
    estimate_pi(n=10_000_000)

profiler.print()
# profiler.open_in_browser()

🦜 Profiling

• Use {profvis}
• Examples
• Visualising profiles in R

Performance Tweaks

Object growth

It starts small… 🥎

• {fig-alt=“A garage full of bikes and sports equipment .fragment width=”70%}

🐍 Pre-allocating Arrays

from timeit import timeit
import numpy as np

size = 100_000

def growing_list():
    result = []
    for i in range(size):
        result.append(i**2)
    return result

def preallocated_array():
    result = np.zeros(size, dtype=int)
    for i in range(size):
        result[i] = i**2
    return result

t1 = timeit(growing_list, number=100)
t2 = timeit(preallocated_array, number=100)
print(f"Growing list: {t1:.6f}s\nPre-allocated: {t2:.6f}s")
print(f"Speedup: {t2/t1:.1f}x faster")

🦜 Pre-allocating Arrays

n	1	2
10^5	0.208	0.024
10^6	25.50	0.220
10^7	3827	2.212

Appropriate Data Structures

• NumPy array faster than a Python list
• Set is much faster than list* but only keeps unique elements
• Just doing numeric calculations? Can you use a matrix?

🐍 Appropriate Data Structures

Data Structure	Mutability	Use Cases	Performance
List	Mutable	Ordered collections	Moderate
Tuple	Immutable	Fixed collections	Fast
Dictionary	Mutable	KV pairs, fast lookups	Fast
Set	Mutable	Unique collections	Fast
NumPy Array	Mutable	Numerical data, math. ops	Very Fast

Loops vs. Vectorisation vs. …

🐍 Loops

from timeit import timeit

size = 64

def standard_loop():
    result = []
    for i in range(size):
        result.append(2**i)
    return result

def list_comprehension():
    return [2**i for i in range(size)]

t1 = timeit(standard_loop, number=100)
t2 = timeit(list_comprehension, number=100)

print(f"Standard loop: {t1:.6f}s\nList comprehension: {t2:.6f}s")
print(f"Speedup: {t1/t2:.1f}x faster")

🐍 Vectorisation with NumPy

from timeit import timeit
import numpy as np

size = 100_000

def python_way():
    return [i**2 for i in range(size)]

def numpy_way():
    return np.arange(size)**2 # Uses C implementation

t1 = timeit(python_way, number=100)
t2 = timeit(numpy_way, number=100)

print(f"Python: {t1:.6f}s\nNumPy: {t2:.6f}s")
print(f"Speedup: {t1/t2:.1f}x faster")

🐍 Vectorisation with Pandas

import pandas as pd
import numpy as np
from timeit import timeit

df = pd.DataFrame({"value": np.random.rand(10_000)})

def apply_method():
    return df["value"].apply(lambda x: x**2)

def vector_method():
    return df["value"]**2

# Compare execution times
t1 = timeit(apply_method, number=100)
t2 = timeit(vector_method, number=100)

print(f"apply: {t1:.6f}s\nvectorised: {t2:.6f}s")
print(f"Speedup: {t1/t2:.1f}x faster")

🦜 Vectorisation

🐍 Functional Programming

from timeit import timeit

size = 100_000

t1 = timeit(lambda: list(map(lambda x: x**2, range(size))), number=100)
t2 = timeit(lambda: [x**2 for x in range(size)], number=100)

print(f"map: {t1:.6f}s\ncomprehension: {t2:.6f}s")
print(f"Speedup: {t1/t2:.1f}x faster")

🐍 Generators

# Generator
def count_up_to(limit):
    count = 0
    while count < limit:
        yield count
        count += 1

print([n for n in count_up_to(50)])

When to Use Each Approach

Approach	Best For	Example Use Case
Loops	Complex logic, small data	Custom algorithms
Vectorisation	Numerical operations	Data science, NumPy
Functional	Data transformations	Pipelines, filter/map/reduce
List Comprehensions	Simple transformations	Filter elements
Generators	Large dataset processing	Read large files line by line

Loop Optimisation

Optimisation Techniques

• Define anything you can outside the loop
• Consider locally assigning common functions
• I/O slows loops
• Look out for print or plot
• Use flag for “chatty” / “quiet”
• Proper logging instead of printing

🐍 Optimisation Techniques

from timeit import timeit
import math
from random import randint

size = 300_000

data = [2**randint(0, 64) for _ in range(size)]

def regular_loop():
    result = 0
    for i in range(len(data)):
        x = data[i]
        result += math.sqrt(x) + math.sin(x) + math.cos(x)
    return result

def optimised_loop():
    result = 0
    n = len(data)
    sqrt, sin, cos = math.sqrt, math.sin, math.cos
    for i in range(n):
        x = data[i]
        result += sqrt(x) + sin(x) + cos(x)
    return result

t1 = timeit(regular_loop, number=100)
t2 = timeit(optimised_loop, number=100)
print(f"Regular: {t1:.6f}s\nOptimised: {t2:.6f}s")
print(f"Speedup: {t1/t2:.1f}x faster")

🦜 Optimisation Techniques

Beyond the Basics

Rewrite in C++

• If you’ve got a function which is a real bottleneck consider rewriting it in C++

• 🐍 Cython to connect C++ and python

• 🦜 {rcpp} to connect C++ and R

🐍 Just-In-Time Compilation (1)

from numba import jit
import numpy as np
from timeit import timeit

def slow_func(x):
    total = 0
    for i in range(len(x)):
        total += np.sin(x[i]) * np.cos(x[i])
    return total

@jit(nopython=True)
def fast_func(x):
    total = 0
    for i in range(len(x)):
        total += np.sin(x[i]) * np.cos(x[i])
    return total

x = np.random.random(10_000)
t1 = timeit(lambda: slow_func(x), number=100)
t2 = timeit(lambda: fast_func(x), number=100)
print(f"Python: {t1:.6f}s\nNumba: {t2:.6f}s")
print(f"Speedup: {t1/t2:.1f}x faster")

🐍 Just-In-Time Compilation (2)

What is JIT?

JIT (Just-In-Time) compilation translates code into machine code at runtime to improve execution speed. This approach can improve performance by optimising the execution of frequently run code segments.

Key Benefits: - Can provide 10-100x speed-ups for numerical code - Works especially well with NumPy operations - Requires minimal code changes (just add decorators)

Parallel processing

Pros

• Larger datasets

• Speed

• It’s easy to set up

Cons

• Debugging is harder

• Can be OS specific

• Many statistical techniques are fundamentally serial

• Can be slower than serial execution due to overheads

Best Practices Summary

1. Measure first - profile before optimising
2. Use appropriate data structures for the task
3. Vectorise numerical operations when possible
4. Avoid premature optimisation - readable code first
5. Know when to use loops, comprehensions, or functional styles

📚 Resources

• Efficient R
• Effective Python, The Book: Third Edition
• Advanced R
• Python data structures
• Functional programming in Python? by David Vujic
• Python profiling

Appendix

Appendix: Cython (Basics)

Pure Python version (slow.py):

def calculate_sum(n):
    """Sum the squares from 0 to n-1"""
    total = 0
    for i in range(n):
        total += i * i
    return total

Cython version (fast.pyx):

def calculate_sum_cy(int n):
    """Same function with static typing"""
    cdef int i, total = 0  # Static type declarations
    for i in range(n):
        total += i * i
    return total

Result: Typically 20-100x faster performance

Appendix: Cython (Best Practices)

Key techniques for maximum performance:

# 1. Declare types for all variables
cdef:
    int i, n = 10_000  # Integer variables
    double x = 0.5   # Floating point
    int* ptr         # C pointer

# 2. Use typed memoryviews for arrays (faster than NumPy)
def process(double[:] arr):  # Works with any array-like object
    cdef int i
    for i in range(arr.shape[0]):
        arr[i] = arr[i] * 2  # Direct memory access

# 3. Move Python operations outside loops
cdef double total = 0
py_func = some_python_function  # Store reference outside loop
for i in range(n):
    total += c_only_operations(i)

# 4. Use nogil for parallel execution with OpenMP
cpdef process_parallel(double[:] data) nogil:  # No Python GIL
    # Can now use OpenMP for parallelism

Appendix: Cython (Compiling)

Option 1: Using setuptools (recommended for projects)

# Create setup.py in your project directory:
from setuptools import setup, Extension
from Cython.Build import cythonize

setup(
    ext_modules = cythonize([
        Extension("fast", ["fast.pyx"]),
    ])
)

# Then compile: python setup.py build_ext --inplace

Option 2: Quick development with pyximport

import pyximport
pyximport.install()  # Automatically compiles .pyx files
import fast  # Will compile fast.pyx on first import

Option 3: Direct compilation

cython -a fast.pyx  # Generates fast.c and HTML report
gcc -shared -fPIC -o fast.so fast.c \
    $(python3-config --includes) $(python3-config --ldflags)